Dark Matters about Metro-Haul

One of the delightful aspects about European research in H2020 is the chance to interact and work with a fantastic set of engineers, scientists, and technologists on interesting and highly worthwhile projects. In justifying the work we do in these research projects, however, there is still always the need to report on the positive impact of the research outcomes. That said, predicting the net positive benefits of research tends to be quite hit and miss; or rather, the benefits can often be surprising and unexpected.

For example, who could have predicted that fundamental particles research at CERN would spawn the World Wide Web and Internet as we now know it 30 years on? Or indeed, somewhat more prosaically, the invention of the non-stick frying pan would result from the moon landings of 50 years ago?

The same is true of some of the optical research I’ve been involved with in recent years. The Metro-Haul project is researching the impact of photonic, virtualised, and software-defined technologies on 5G networking: each of these technologies representing critical paths towards the ubiquitous multi-Gb/s, millisecond latencies, and low energy consumption that 5G is promising. And, of course, Metro-Haul is also the successful outcome of an earlier H2020 project, IDEALIST, that researched into the optical technologies required for agile, adaptive, and elastic optical networking.

A key research topic of photonic networking in IDEALIST and continuing into Metro-Haul relates to the efficient use of the optical spectrum; that is, optimising what is known as routing and spectrum assignment (RSA) to avoid fragmenting the available capacity of an optical fibre. And the best metric for understanding the fragmentation of a resource is to study its entropy. Working together with Andrew Lord (Metro-Haul’s Coordinator) and Paul Wright at BT we found that by employing Maximum Entropy (MaxEnt) techniques we could significantly improve the efficiency of an optical network and greatly expand its throughput.

In using Maximum Entropy to analyse the performance of an optical network, we also discovered it was revealing important yet ‘hidden’ details about the network. We found MaxEnt could also be used as a tool to see where network hot spots are located and where adding additional fibre would be most cost-advantageous to increase capacity. Not only that, when Deutsche Telekom (who were also partners in IDEALIST) used the Maximum Entropy technique to analyse their network, they discovered that even though almost 30 years had already elapsed since German reunification, unbeknownst to them their network still bore indelible traces of that historical East-West divide – this despite massive investment in upgrading and modernising their telecoms infrastructure.

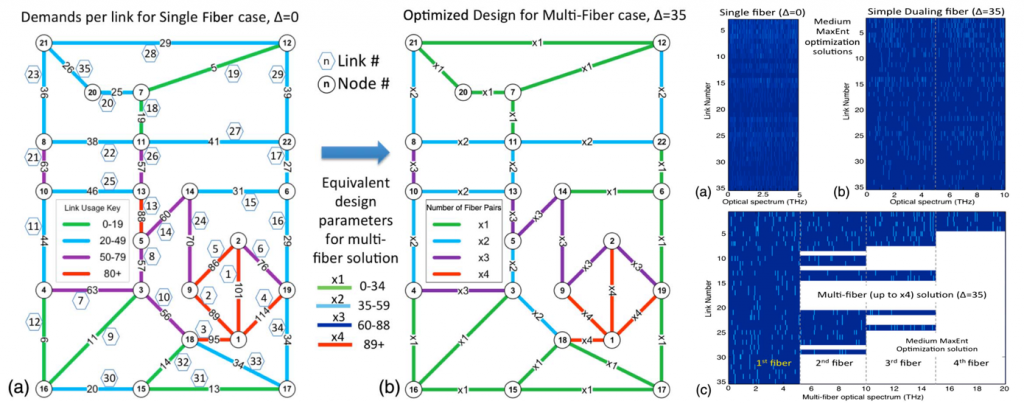
Figure 1: Application of Maximum Entropy techniques to optimise the BT Network [1].

The power of Maximum Entropy set me thinking about whether this apparently purely mathematical and abstract tool could also be applied to rather less technological and maybe rather more ‘natural scientific’ matters: I was interested in investigating whether MaxEnt could be applied to the shapes and geometries seen every day in Nature. I had already noticed a seeming preference in Nature for shapes such as helices and spirals, e.g., snail shells, the arrangement of seeds in sunflowers, biomolecules, even the Mandelbrot set. I wondered whether Maximum Entropy theory could perhaps be applied to these structures and used to prove that these shapes are indeed the ‘most likely’ (which is a synonym of ‘MaxEnt’) to be adopted by Nature.

This set me on a path lasting a few years while I investigated and unravelled the equations underpinning the application of Maximum Entropy to the natural world. The result was very surprising – I had discovered an entirely parallel universe to the one that science has hitherto explored.

Students of the history of science know all the various scientific discoveries that have led to the remarkable modern age of information, computing, and technology that we enjoy today. However, as currently understood by the vast majority of scientists (and particularly physicists) the existing state of scientific knowledge about the physical world is encapsulated by a single concept: the Principle of Least Action. As Max Planck put it back in 1915, “The Principle of Least Action…dominates all of mechanics as well as all other physics,” and as Richard Feynman put it in 1948, “All of mechanics and electrodynamics is contained in this single variational principle.” It also underpins General Relativity as well as Quantum Mechanics via the Schrödinger Equation.

It would appear that the Principle of Least Action, based on the quantum of action, the Planck constant, is all that is required to analyse and understand the physical world. However, as Metro-Haul engineers, scientists and technologists researching to ever improve and extend this current Age of Information into the Age of 5G and beyond, we know that this is perhaps not completely true – you see, we use Claude Shannon as our leading guide with his entropy theory of information, which is based upon the Boltzmann constant k_B as its fundamental physical unit. As ICT technologists, we are already at ease with thinking that information and entropy don’t necessarily obey the Principle of Least Action. Of course, we also have to realise that information is actually a physical quantity. It’s interesting to see how many people still think that information is merely an ‘abstract’ quantity with only mathematical properties and no real bearing on the physical world. But when you see cosmologists like Stephen Hawking actively trying to understand whether information is conserved when swallowed up by a black hole, then you might start realising that perhaps there is something real and physical to information after all!

Back to my discovery, I found there exists a parallel law to the Principle of Least Action, but based on info-entropy and employing the Boltzmann constant as its quantum unit. I decided to call my discovery the Principle of Least Exertion, as a subtle echo of least action. Rather interestingly, it obeys its own variational calculus Euler-Lagrange equation (which means that Emmy Nöther’s theorem also applies – the implication being that there are various conserved quantities associated with entropy and information as well. But perhaps that’s a discussion for another time!)

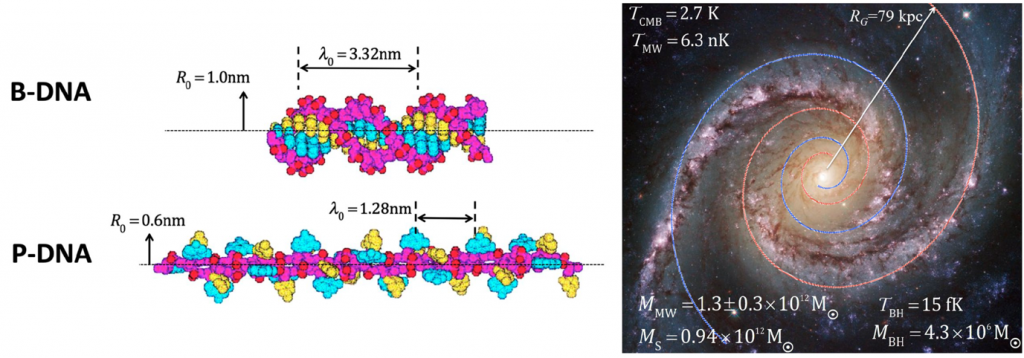
Figure 2: Application of Maximum Entropy theory to DNA and the Milky Way galaxy [2].

A pretty mathematical theory is all well and good, but does it actually have any bearing on our physical, natural world? This is always the key scientific question for any theory: Does it correctly predict or explain behaviour observed in the real world? Working with another colleague Chris Jeynes from the University of Surrey, UK, we scoured the literature for examples of systems which had the necessary features and parameters that could be used to quantitatively assess our Quantitative Geometric Thermodynamics (QGT) theory. We alighted on DNA and the Milky Way galaxy. In some extraordinary work from 2003 we found an experiment where DNA was twisted under tension using optical tweezers to reshape it from its conventional B-DNA form into a longer, thinner form of the double-helical molecule. Exquisite precision was the hallmark of the experiment and, taking everything into account, the experimentalists found that 1151 aJ (that’s 10^-18 J!) was required to transform the DNA molecule into its alternative, stringier form. Very heavy computational effort is required to calculate such a result using the existing energy-based numerical models; however, our entropy approach enables a simple back-of-the-envelope calculation to quickly yield a value of 1184 aJ. Well within the 70 aJ experimental uncertainties associated with the actual experiment!

Next, we applied the entropy theory to our galaxy – the Milky Way. First of all, our entropy theory explains why the Milky Way exhibits a double logarithmic spiral geometry – it’s so as to maximise the entropy of the overall galaxy. But what is the energy associated with such a structure? The calculation is a bit more involved; but having undertaken it we discovered that the energy calculated is equivalent (when converted using Einstein’s famous mass-energy equivalence equation, E=mc²) to about a trillion solar masses. This is both a very large number, but also about a factor of 10 times higher than the observed mass of all the 100 billion stars in our galaxy. In fact, the total mass we calculated is also the same as the so-called Dark Matter in our galaxy. This was an interesting result, and worthy of further investigation.

Actually, another interesting aspect of our research was answering the question of where all the galactic entropy comes from. It turns out that Stephen Hawking and Jakob Bekenstein had already answered that question some 45 years ago: the largest source of entropy in our galaxy is the supermassive black hole found at the centre of the Milky Way, weighing in at a hefty 4.2 million suns. Bekenstein and Hawking famously found that the entropy of a black hole is proportional to the surface area of the ‘event horizon’, the point at the Schwarzschild radius beyond which even light can no longer escape the gravitational pull of a black hole. However, whereas conventional science assumes that the black hole’s entropy simply lies ‘passively’ at the surface of the event horizon, our theory conclusively shows that the entropy exerts its influence far beyond the conventional confines of the Schwarzschild radius. How can this be? Well, it’s because the Boltzmann constant is an independent physical constant of nature as compared to the Planck constant. Whereas all of kinematics, energy, mass, even the equations of general relativity are based on the Principle of Least Action and a Lagrangian denominated in the quantum of action (Planck’s constant), entropy having a very different fundamental unit (J/K, joules per unit temperature) obeys the Principle of Least Exertion and isn’t bound by these kinematic laws; entropy follows a complementary set of laws so that it isn’t confined to the black hole as energy and mass are.

Even though it’s ‘supermassive’ at 4.2 million suns, compared to the overall weight of the galaxy of a trillion suns, it’s clear that the Milky Way’s central black hole is far too ‘small’ to hold the galaxy together via gravity – hence the need for ‘dark matter’. And that’s why astrophysicists also tend to completely disregard the existence of a supermassive black hole at the galactic centre – to them, it’s just a ‘coincidence’ that it happens to be there in the middle – it’s far too small to be of any significance to the galaxy! But, when you understand the role of entropy in the structure and stability of a galaxy, it suddenly becomes quite clear: it’s the entropy from the supermassive black hole at the galactic centre that is holding the galaxy together! Dark matter is no longer required!

Astronomers and physicists are now grappling with the results of our paper [2] recently published in the journal Scientific Reports, which is part of the Nature stable of titles. To be honest, given their rather sceptical comments (e.g., see the comments section following a more accessible and popular science article we wrote describing our work [3]) it’s clear it’s going to take a while for our new entropy theory to be understood, let alone accepted. That’s also true for chemists, molecular biologists, and scientists in other disciplines, where this new entropy theory also finds important application. Entropy has always been a rather ‘difficult’ concept for people to understand. Indeed, that’s why John von Neumann (inventor of the basic architecture of computers) whimsically suggested to Claude Shannon to call the new theoretical quantity he’d discovered “information entropy”; precisely because, as von Neumann quipped, “no-one understands entropy!”

So, where does that leave us? Starting out from optimising BT’s and Deutsche Telekom’s photonic networks, I’ve discovered a completely new scientific principle organising the natural world: the Principle of Least Exertion. Unfortunately, because I did this work in my spare time, I wasn’t able to give Metro-Haul (let alone, belatedly, IDEALIST) a formal acknowledgement in my paper, which I feel a bit sad about. But I also wasn’t sure whether our Project Officer would be impressed to see a paper about DNA and black holes as a Metro-Haul output! However, I think this entropy work has continued in an honourable tradition of interesting and innovative research emerging from the most unexpected directions; indeed, telecoms research has frequently led in the past to many of the most important and fundamental discoveries. Long may this tradition of innovative European collaborative research continue!

References